En la mecánica newtoniana, para un cuerpo con
masa constante, la aceleración del cuerpo es proporcional a la
fuerza que actúa sobre el mismo (
segunda ley de Newton):
donde
F es la fuerza resultante que actúa sobre el cuerpo,
m es la
masa del cuerpo, y
a es la aceleración. La relación anterior es válida en cualquier
sistema de referencia inercial.
Introducción[editar]
De acuerdo con la
mecánica newtoniana, una partícula no puede seguir una trayectoria curva a menos que sobre ella actúe una cierta aceleración como consecuencia de la acción de una fuerza, ya que si esta no existiese, su movimiento sería rectilíneo. Asimismo, una partícula en movimiento rectilíneo solo puede cambiar su
velocidad bajo la acción de una aceleración en la misma dirección de su velocidad (dirigida en el mismo sentido si acelera; o en sentido contrario si desacelera).
Algunos ejemplos del concepto de aceleración son:
- La llamada aceleración de la gravedad en la Tierra es la aceleración que produce la fuerza gravitatoria terrestre; su valor en la superficie de la Tierra es, aproximadamente, de 9,8 m/s2. Esto quiere decir que si se dejara caer libremente un objeto, aumentaría su velocidad de caída a razón de 9,8 m/s por cadasegundo (siempre que omitamos la resistencia aerodinámica del aire). El objeto caería, por tanto, cada vez más rápido, respondiendo dicha velocidad a la ecuación:
- Una maniobra de frenada de un vehículo, que se correspondería con una aceleración de signo negativo, o desaceleración, al oponerse a la velocidad que ya tenía el vehículo. Si el vehículo adquiriese más velocidad, a dicho efecto se le llamaría aceleración y, en este caso, sería de signo positivo.
Aceleración media e instantánea[editar]

Definición de la aceleración de una partícula en un movimiento cualquiera. Obsérvese que la aceleración no es tangente a la trayectoria.
Cada instante, o sea en cada punto de la
trayectoria, queda definido un vector velocidad que, en general, cambia tanto en módulo como en dirección al pasar de un punto a otro de la trayectoria. La dirección de la velocidad cambiará debido a que la velocidad es tangente a la trayectoria y esta, por lo general, no es rectilínea. En la Figura se representan los vectores velocidad correspondientes a los instantes
t y
t+Δ
t, cuando la partícula pasa por los puntos P y Q, respectivamente. El cambio vectorial en la velocidad de la partícula durante ese intervalo de tiempo está indicado por Δ
v, en el triángulo vectorial al pie de la figura. Se define la
aceleración media de la partícula, en el intervalo de tiempo Δ
t, como el cociente:
Que es un vector paralelo a Δ
v y dependerá de la duración del intervalo de tiempo Δ
t considerado. La aceleración instantánea se la define como el límite al que tiende el cociente incremental Δ
v/Δ
t cuando Δ
t→0; esto es la
derivada del vector velocidad con respecto al tiempo:
Puesto que la velocidad instantánea
v a su vez es la derivada del vector
posición r respecto al tiempo, la aceleración es la derivada segunda de la posición con respecto del tiempo:
De igual forma se puede definir la velocidad instantánea a partir de la aceleración como:
Se puede obtener la velocidad a partir de la aceleración mediante
integración:
Medición de la aceleración[editar]
La medida de la aceleración puede hacerse con un sistema de adquisición de datos y un simple
acelerómetro. Los acelerómetros electrónicos son fabricados para medir la aceleración en una, dos o tres direcciones. Cuentan con dos elementos conductivos, separados por un material que varia su conductividad en función de las medidas, que a su vez serán relativas a la aceleración del conjunto.
Las unidades de la aceleración son:
- 1 m/s2
- 1 cm/s2 = 1 Gal
Componentes intrínsecas de la aceleración: aceleraciones tangencial y normal[editar]
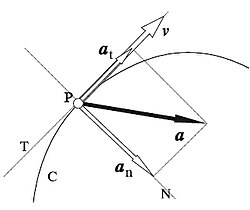
Componentes intrínsecas de la aceleración.
En tanto que el vector velocidad
v es tangente a la trayectoria, el vector aceleración
a puede descomponerse en dos componentes (llamadas componentes intrínsecas) mutuamente perpendiculares: una componente tangencial
at (en la dirección de la tangente a la trayectoria), llamada
aceleración tangencial, y una componente normal
an (en la dirección de la normal principal a la trayectoria), llamada
aceleración normal o
centrípeta (este último nombre en razón a que siempre está dirigida hacia el centro de curvatura).
Derivando la velocidad con respecto al tiempo, teniendo en cuenta que el vector tangente cambia de dirección al pasar de un punto a otro de la trayectoria (esto significa que no es constante) obtenemos
siendo
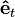
el
vector unitario tangente a la trayectoria en la misma dirección que la velocidad y

la velocidad angular. Resulta conveniente escribir la expresión anterior en la forma
siendo
 el vector unitario normal a la trayectoria, esto es dirigido hacia el centro de curvatura de la misma,
el vector unitario normal a la trayectoria, esto es dirigido hacia el centro de curvatura de la misma, el radio de curvatura de la trayectoria, esto es el radio de la circunferencia osculatriz a la trayectoria.
el radio de curvatura de la trayectoria, esto es el radio de la circunferencia osculatriz a la trayectoria.
Las magnitudes de estas dos componentes de la aceleración son:
Cada una de estas dos componentes de la aceleración tiene un significado físico bien definido. Cuando una partícula se mueve, su
velocidad puede cambiar y este cambio lo mide la aceleración tangencial. Pero si la trayectoria es curva también cambia la dirección de la velocidad y este cambio lo mide la aceleración normal.
- Si en el movimiento curvilíneo la velocidad es constante (v=cte), la aceleración tangencial será nula, pero habrá una cierta aceleración normal, de modo que en un movimiento curvilíneo siempre habrá aceleración.
- Si el movimiento es circular, entonces el radio de curvatura es el radio R de la circunferencia y la aceleración normal se escribe como an = v2/R.
- Si la trayectoria es rectilínea, entonces el radio de curvatura es infinito (ρ→∞) de modo que an=0 (no hay cambio en la dirección de la velocidad) y la aceleración tangencial at será nula o no según que la velocidad sea o no constante.
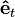 es el vector unitario tangente a la curva.
es el vector unitario tangente a la curva. es el vector unitario normal a la curva.
es el vector unitario normal a la curva. es el vector velocidad angular que es paralelo al vector binormal a la curva.
es el vector velocidad angular que es paralelo al vector binormal a la curva.
Movimiento circular uniforme[editar]

Cinemática del movimiento circular.
Un movimiento circular uniforme es aquel en el que la partícula recorre una trayectoria circular de radio R con velocidad constante, es decir, que la distancia recorrida en cada intervalo de tiempo igual es la misma. Para ese tipo de movimiento el vector de velocidad mantiene su módulo y va variando la dirección siguiendo una trayectoria circular. Si se aplican las fórmulas anteriores, se tiene que la aceleración tangencial es nula y la aceleración normal es constante: a esta aceleración normal se la llama "aceleración centrípeta". En este tipo de movimiento la aceleración aplicada al objeto se encarga de modificar la trayectoria del objeto y no en modificar su velocidad.
Movimiento rectilíneo acelerado[editar]

En el Movimiento Rectilíneo Acelerado, la aceleración instantánea queda representada como la pendiente de la recta tangente a la curva que representa gráficamente la función
v(
t).
Si se aplican las fórmulas anteriores al movimiento rectilíneo, en el que solo existe aceleración tangencial, al estar todos los vectores contenidos en la trayectoria, podemos prescindir de la notación vectorial y escribir simplemente:
Ya que en ese tipo de movimiento los vectores

y

son paralelos, satisfaciendo también la relación:
La coordenadas de posición viene dada en este caso por:
Un caso particular de movimiento rectilíneo acelerado es el
movimiento rectilíneo uniformemente variado donde la aceleración es además constante y por tanto la velocidad y la coordenadas de posición vienen dados por:
Aceleración en mecánica relativista[editar]
Relatividad especial[editar]
El análogo de la aceleración en
mecánica relativista se llama cuadriaceleración y es un
cuadrivector cuyas tres componentes espaciales para pequeñas velocidades coinciden con las de la aceleración newtoniana (la componente temporal para pequeñas velocidades resulta proporcional a la potencia de la fuerza dividida por la velocidad de la luz y la masa de la partícula).
En mecánica relativista la cuadrivelocidad y la cuadriaceleración son siempre ortogonales, eso se sigue de que la cuadrivelocidad tiene un (pseudo)módulo constante:
Donde
c es la velocidad de la luz y el producto anterior es el producto asociado a la
métrica de Minkowski:
Relatividad general[editar]
En
teoría general de la relatividad el caso de la aceleración es más complicado, ya que debido a que el propio
espacio-tiempo es curvo (ver
curvatura del espacio-tiempo), una partícula sobre la que no actúa ninguna fuerza puede seguir una trayectoria curva, de hecho la línea curva que sigue una partícula sobre la que no actúa ninguna fuerza exterior es una línea
geodésica, de hecho en relatividad general la fuerza gravitatoria no se interpeta como una fuerza sino como un efecto de la curvatura del espacio-tiempo que hace que las partículas no trayectorias rectas sino líneas geodéscias. En este contexto la aceleración no geodésica de una partícula es un vector cuyas cuatro componentes se calulan como:
Aquí

(componente temporal y tres componentes espaciales). Se aprecia que cuando los
símbolos de Christoffel 
una partícula puede tener aceleración cero aunque su cuadrivelocidad no sea constante, eso sucede cuando la partícula sigue una línea geodésica de un espacio-tiempo de curvatura no nula.
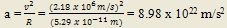 Ejemplo. Una partícula P viaja a velocidad constante en un círculo de 3 m de radio y completa una revolución en 20 s (véase la figura). a) encuentre el valor de la aceleración; b) la rapidez con la que viaja.
Ejemplo. Una partícula P viaja a velocidad constante en un círculo de 3 m de radio y completa una revolución en 20 s (véase la figura). a) encuentre el valor de la aceleración; b) la rapidez con la que viaja.
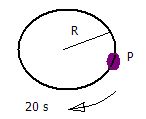 a) Los datos dados son el período T y la velocidad de la partícula, con ellos, se puede obtener la aceleración:
a) Los datos dados son el período T y la velocidad de la partícula, con ellos, se puede obtener la aceleración:
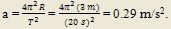 b) La rapidez se encuentra mediante la relación de la aceleración y el radio:
b) La rapidez se encuentra mediante la relación de la aceleración y el radio:
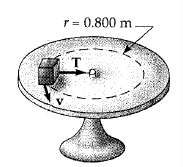
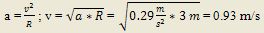 Ejemplo. Un astronauta está girando en una centrífuga de 5.2 m de radio. a) ¿Cuál es su velocidad si la aceleración es de 6.8 g?; b)¿Cuántas revoluciones por minuto se requieren para producir ésa aceleración?.
a) Se sabe que el valor de g es el de la aceleración de la gravedad (9.8 m/s^2). Entonces:
Ejemplo. Un astronauta está girando en una centrífuga de 5.2 m de radio. a) ¿Cuál es su velocidad si la aceleración es de 6.8 g?; b)¿Cuántas revoluciones por minuto se requieren para producir ésa aceleración?.
a) Se sabe que el valor de g es el de la aceleración de la gravedad (9.8 m/s^2). Entonces:
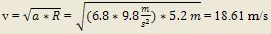 b) El período T se encuentra:
b) El período T se encuentra:
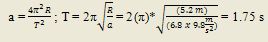 Por definición: 1 revolución se da en 1.75 s, entonces:
Por definición: 1 revolución se da en 1.75 s, entonces:
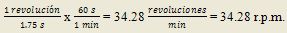 En el movimiento circular general, al inverso del período se le conoce como frecuencia.
En el movimiento circular general, al inverso del período se le conoce como frecuencia.
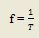 donde f es la frecuencia (número de vueltas por unidad de tiempo) y sus unidades son 1/s.
donde f es la frecuencia (número de vueltas por unidad de tiempo) y sus unidades son 1/s.
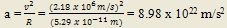

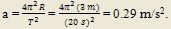
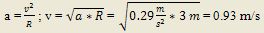
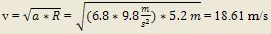
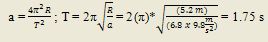
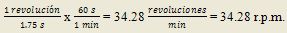
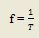












 o
o  y su
y su  . Sus dimensiones son
. Sus dimensiones son ![\scriptstyle [ L \cdot T^{-2} ]](https://upload.wikimedia.org/math/8/d/9/8d93fafc52fa31cdcc17a888d15c7165.png) . Su unidad en el
. Su unidad en el 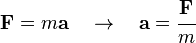



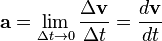
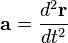




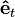 el vector unitario tangente a la trayectoria en la misma dirección que la velocidad y
el vector unitario tangente a la trayectoria en la misma dirección que la velocidad y  la velocidad angular. Resulta conveniente escribir la expresión anterior en la forma
la velocidad angular. Resulta conveniente escribir la expresión anterior en la forma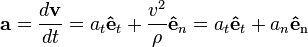
 el vector unitario normal a la trayectoria, esto es dirigido hacia el centro de curvatura de la misma,
el vector unitario normal a la trayectoria, esto es dirigido hacia el centro de curvatura de la misma, el
el 




 y
y  son paralelos, satisfaciendo también la relación:
son paralelos, satisfaciendo también la relación:
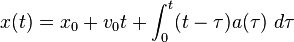

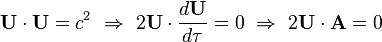


 (componente temporal y tres componentes espaciales). Se aprecia que cuando los
(componente temporal y tres componentes espaciales). Se aprecia que cuando los  una partícula puede tener aceleración cero aunque su cuadrivelocidad no sea constante, eso sucede cuando la partícula sigue una línea geodésica de un espacio-tiempo de curvatura no nula.
una partícula puede tener aceleración cero aunque su cuadrivelocidad no sea constante, eso sucede cuando la partícula sigue una línea geodésica de un espacio-tiempo de curvatura no nula.